物理の計算では必須の三角関数!
物理の力学ではたびたび三角関数を使って計算するでしょう。坂を下っている球体にかかっている力を求めるときや、斜めに放たれた物体の水平方向の速さを求めるときなど、使う機会はたくさんあります。そんな三角関数を一から解説したいとおもいます。
sin cos tanって?
まずはsin(サイン) cos(コサイン) tan(タンジェント)について説明します。まず、下の図のような直角三角形があったとします。
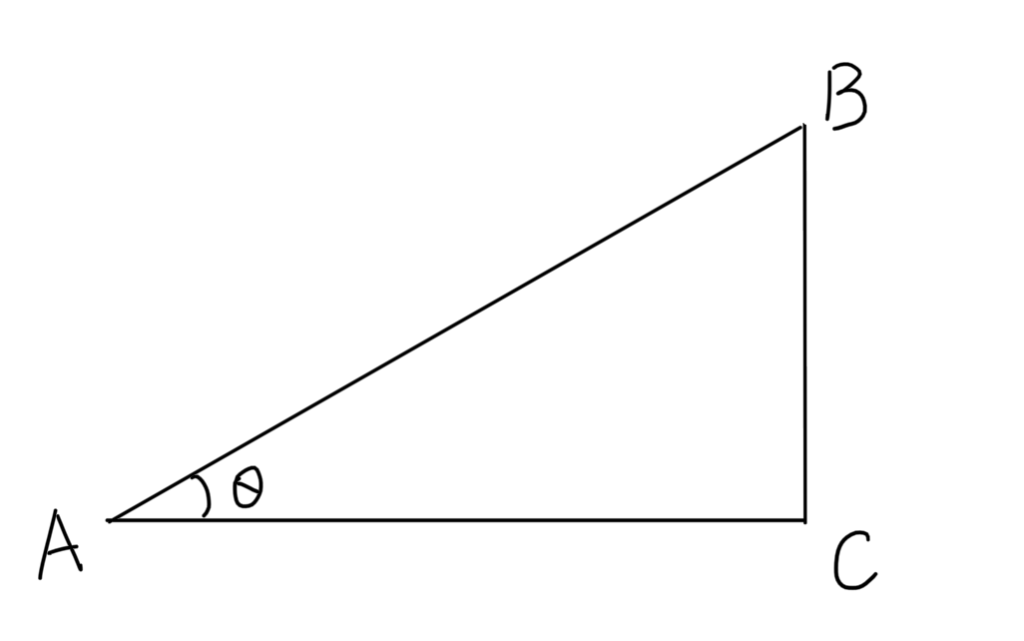
図の頂点Aの角度をθ(シータ)と置いたとき、高さを斜辺で割った数をθの正弦、sinθと言います。また、底辺を斜辺で割った数をθの余弦、cosθと言います。高さを底辺で割った数をθの正接、tanθと言います。要するにこういうことですね。
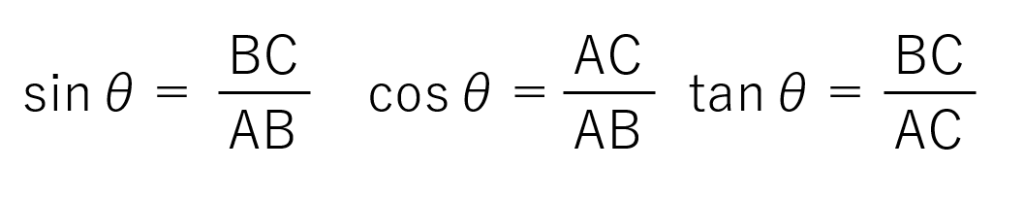
sinθ・cosθ・tanθは以下のような関係性を持っています。
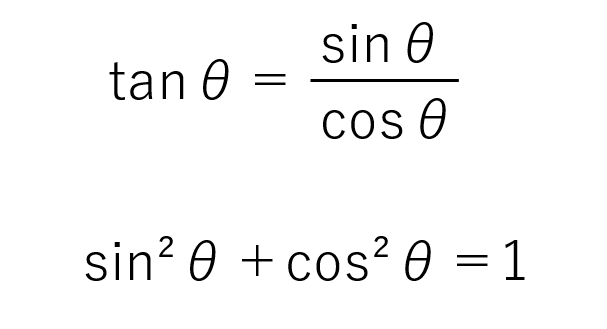
また、二番目の公式は両辺をcosθの二乗で割ることで以下のようなcosθとtanθだけの公式が得られます。ここでは表記しませんが、sinθの二乗で割ることでsinθとtanθだけの公式も得られます。
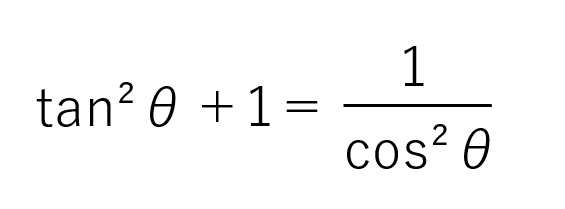
単位円で見る三角関数
単位円は三角関数の値を視覚的に分かりやすくするものです。
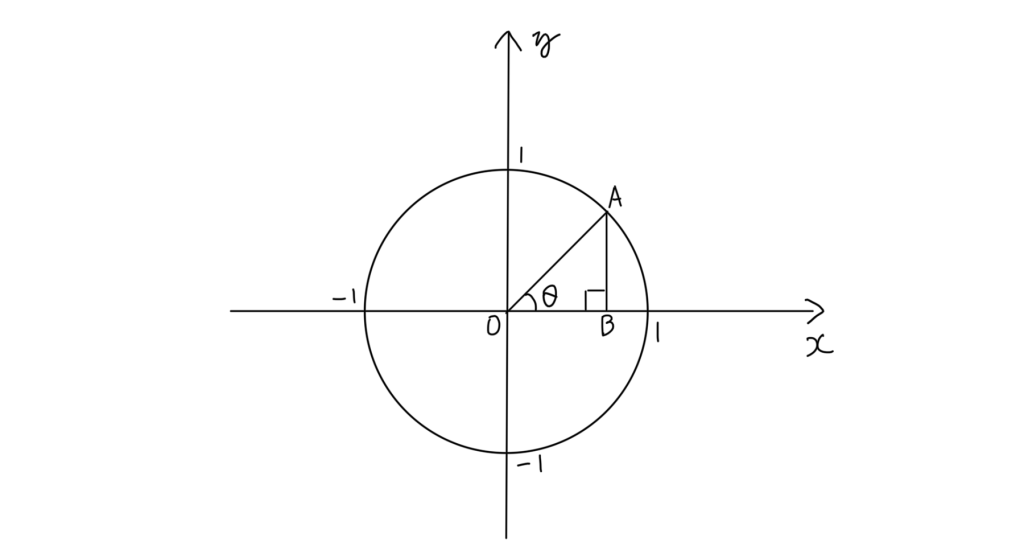
上の図のように、xy軸上に描かれた半径1の円があり、その中に頂点Oの角度がθの三角形があります。このときのsinθ・cosθを求めるとき、斜辺は円の半径なので1です。ということは、sinθ・cosθを求めるときの分母は1になり、sinθ・cosθの値は分子の値になります。sinθは辺ABの長さ、cosθは辺OBの長さになります。図で言うと…
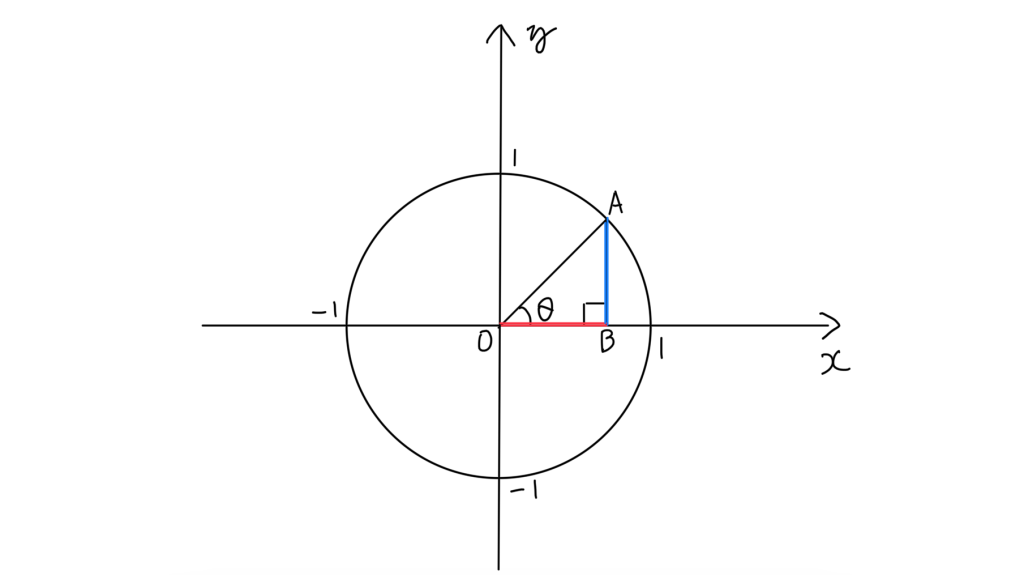
青の長さがsinθで、赤がcosθですね。ちなみにtanθの値は下の図のように、x=1の直線に、斜辺の延長線が交わってできた三角形の高さ(緑の線)です。
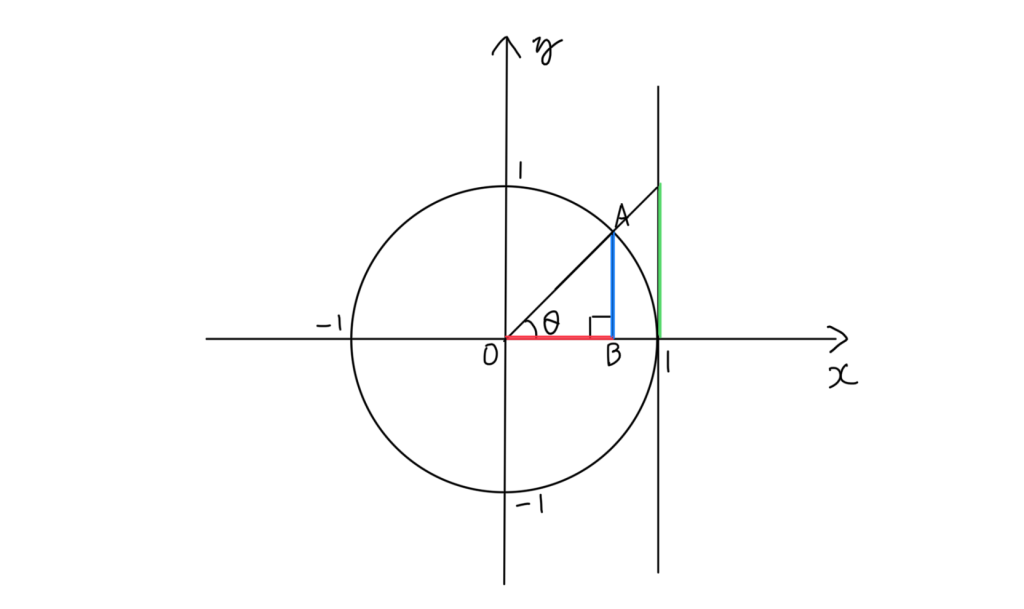
さて、θが0°〜90°なら三角形も直角を含んでいるので分かりやすいんですが、θが90°〜180°の場合はそうはいきません、円の上に描く三角形の頂点Oはθではなくなってしまうので。ですが、下の図を見たらすぐにわかるはずです。
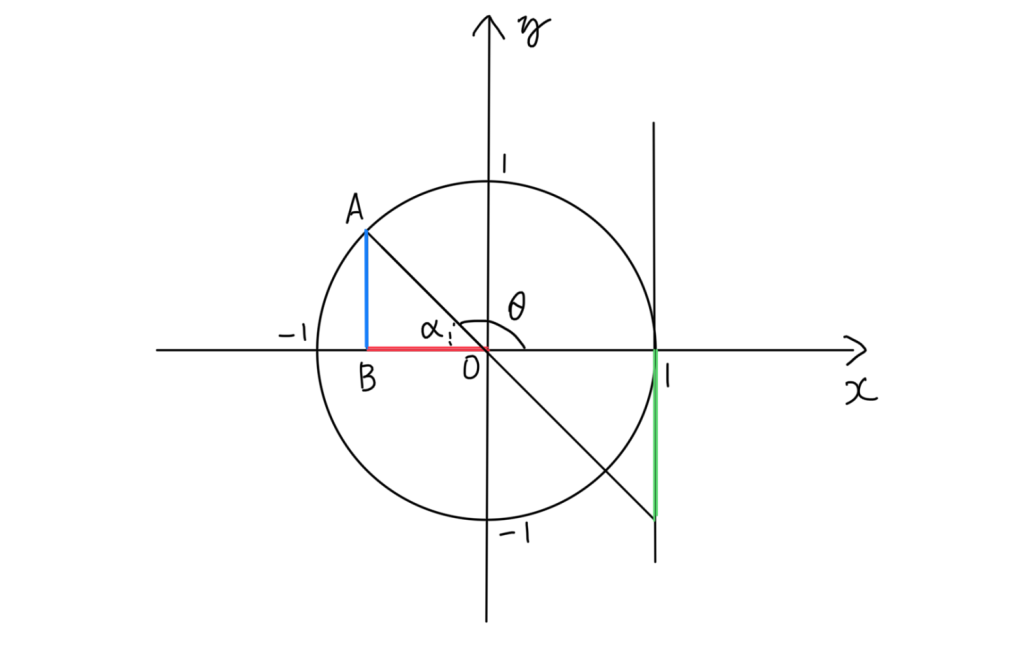
今度は頂点Oの角度をαと置きましょう。置く文字が変わったとしてもsinθ・cosθの値は高さ・底辺ということには変わりありません、ただ変わったのは値の符号です。このときの三角形の底辺はx座標のマイナス側にありますよね。ということはcosθの符号はマイナスになるということです。tanθを表す緑色の線もy軸のマイナス側にあるので、tanθの符号はマイナスになります。つまりこの時、sinα=sinθ cosα=ーcosθ tanα=ーtanθ になります。
180°以上は物理では基本的に使わないと思いますが、イメージをつけるために画像を用意しました。
180°〜270°のとき
sinθ→ー cosθ→ー tanθ→+
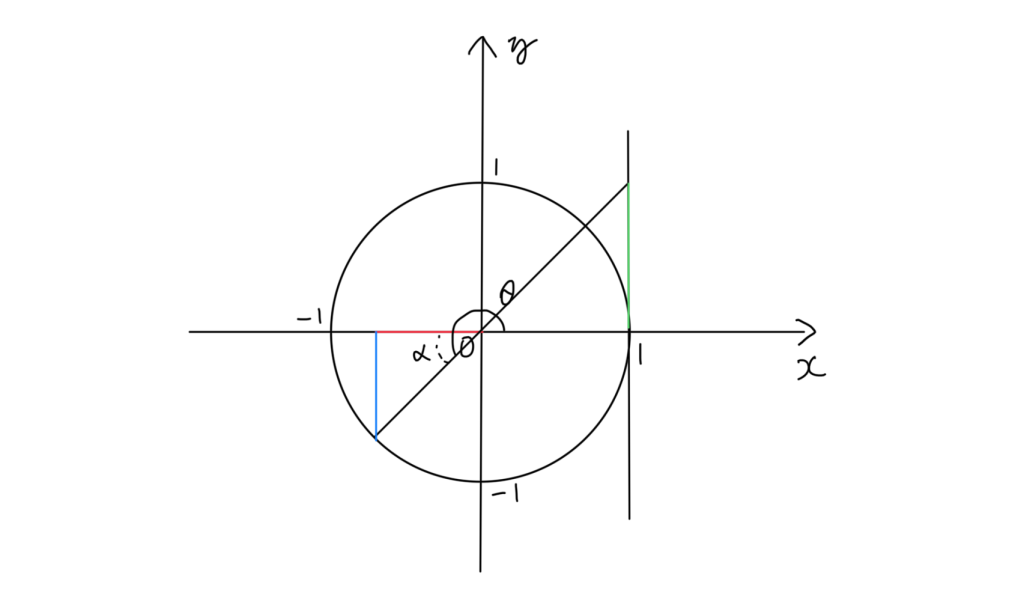
270°〜360°のとき
sinθ→ー cosθ→+ tanθ→ー
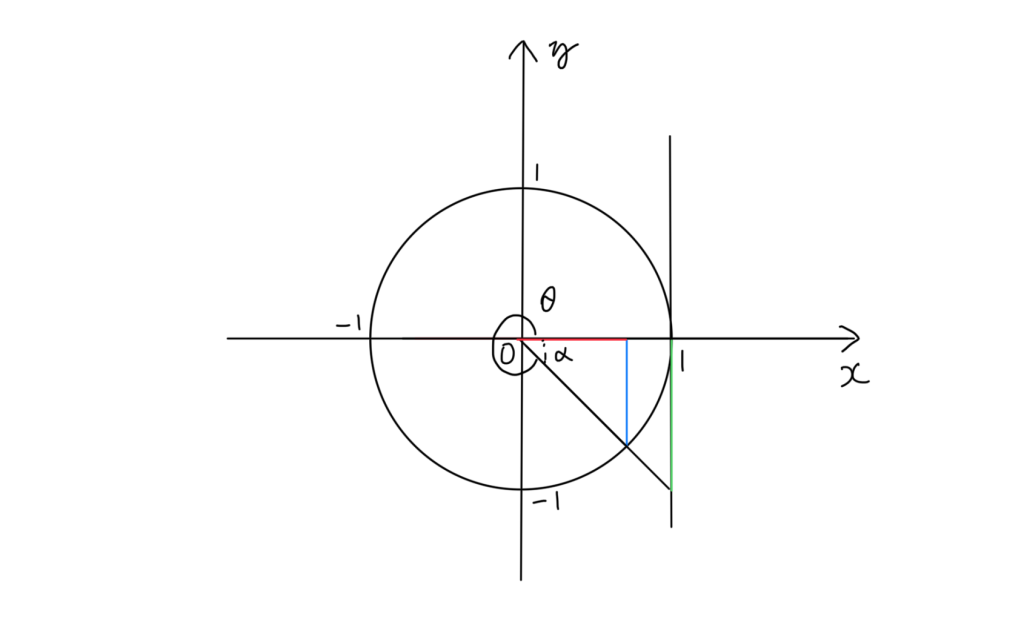
三角関数の値域
単位円は三角関数の大体の値がわかるだけではなく、符号がどっちなのかも分かりますが、この単位円を見て、勘のいい人はsinθ、cosθが特定の範囲しか持たないことに気づいたと思います。単位円の中の三角形は半径1の円の中で動いているだけなので、どの辺も1より大きくなることはないですよね。ということは、sinθもcosθも絶対値は1より大きくなることはないということです。(tanθはどんな値も取る可能性があります。)まぁ、こういうことですね。
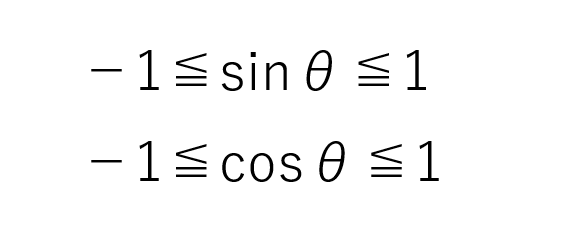
三角関数の有名角
sinθ、cosθ、tanθのθには覚えておくべき角度があります。

※tan90°は存在しません
ここにある角度と値は頻繁に使うものなので必ず覚えておきましょう。
物理で使う三角関数はこの程度で十分でしょう、数学で使う三角関数についてはまた別の機会にしようかなと思います。