熱化学方程式について

　化学変化や状態変化には熱エネルギーの変化がつきものです、普段使っているライターやガスコンロにも、化学変化による熱エネルギーを利用していますからね。では、やっていきましょう！

目次

• 発熱反応と吸熱反応
• 熱化学方程式を書こう
• 反応熱の種類
• ヘスの法則について

発熱反応と吸熱反応

化学変化において、反応後に熱が発生する反応を発熱反応、逆に熱を吸収する反応を吸熱反応といいます。

発熱反応の例

CH₄(メタン)が1mol完全燃焼すると891kJの熱量が発生します。

CH₄＋2O₂→CO₂＋2H₂O (891kJ/molの発熱)

吸熱反応の例

赤熱した1molのC(黒鉛)が水蒸気と反応すると131kJの熱量が吸収されます。

C(黒鉛)＋H₂O→CO＋H₂ (131kJ/molの吸収)

このような、化学変化によって発生または吸収されたりする熱量を反応熱といいます。

ちなみに、1gの水を１℃上げるため必要な熱量は1cal(カロリー)で、1cal＝4.2Jです。

熱化学方程式を書こう

化学変化による熱エネルギーの変化を表すときには、化学反応式ではなく熱化学方程式を用いて表します。作り方は以下の通りです。

まずは熱化学方程式で表したい化学反応式を書きます。今回は水素の燃焼を例とします。

2H₂＋O₂→2H₂O

次に着目する物質の係数を1にします。今回は水素の燃焼に着目しているので、水素の係数を1にするために全ての物質の係数を2で割ります。(このとき他の物質の係数が分数になるときがあります。)

$\mathrm{H₂} ＋\frac{1}{2}\mathrm{O₂} \to \mathrm{H₂O}$

矢印(→)を等号(＝)に変え、反応熱(発熱反応のときの符号は＋、吸熱反応のときの符号は−)を右辺に加えます。

$\mathrm{H₂} ＋\frac{1}{2}\mathrm{O₂} ＝ \mathrm{H₂O} ＋ \mathrm{286kJ}$

物質の状態を明記するためにそれぞれの物質の横に、気体なら(気)、液体なら(液)、固体なら(固)を書き、水溶液に溶けている状態ならaqを加え、水をそのまま使うならaqだけを書きます。

$\mathrm{H₂(気)} ＋\frac{1}{2}\mathrm{O₂(気)}$

$＝ \mathrm{H₂O(液)} ＋ \mathrm{286kJ}$

これで完成ですね。aqについては使うイメージがつかめない人もいるかもしれませんが、aqを使う例は次の溶解熱と中和熱の例で使うので、そちらをご覧ください。

反応熱の種類について

反応熱には、生成熱・燃焼熱・溶解熱・中和熱の４つの種類があります。それぞれ例を紹介しながら説明していこうと思います。

①生成熱

元素の単体から、1molの化合物が生成するときに発生する反応熱を生成熱と言います。

メタン(CH₄)の生成熱は74.9kJです。

$\mathrm{C(黒鉛)} ＋\mathrm{2H₂(気)}$

$＝ \mathrm{CH₄(気)} ＋ \mathrm{74.9kJ}$

②燃焼熱

1molの物質を完全燃焼するときに発生する反応熱を燃焼熱と言います。

メタン(CH₄)の燃焼熱は1561kJです。

$\mathrm{CH₄(気)} ＋\mathrm{2O₂(気)}$

$＝ \mathrm{CO₂(気)} ＋ \mathrm{2H₂O(液)}＋ \mathrm{891kJ}$

③溶解熱

1molの物質を多量の溶媒に溶かしたときに発生する反応熱を溶解熱といいます。

食塩(塩化ナトリウム,NaCl)を水に溶かすと－3.9kJの溶解熱が発生します。

$\mathrm{NaCl(固)} ＋\mathrm{aq}$

$＝ \mathrm{NaClaq} － \mathrm{3.9kJ}$

溶媒として水を使うときにはaqを用いたり、溶解した食塩を表すときに分子式の横にaqをつけたりします。

④中和熱

酸と塩基が中和して水が1mol生成するときに発生する反応熱を中和熱といいます。

塩酸(HCl)と水酸化ナトリウム(NaOH)水溶液との中和反応では、56.5kJの中和熱が発生します。(中和熱はほぼ一定で56.5kJです。)

$\mathrm{HClaq} ＋\mathrm{NaOHaq}$

$＝ \mathrm{NaClaq} ＋\mathrm{H₂O}＋ \mathrm{56.5kJ}$

ヘスの法則について

「反応熱は、反応の経路によらず、反応の初めの終わりの状態で決まる」ことをヘスの法則(総熱量保存の法則)と言います。これだけ聞いてもどういうことだかわかりませんよね・・・

例えば、化学反応がA→B→Cという風に進む反応があったとしましょう。A→Bの反応熱は5kJ、B→Cの反応熱は7kJとしたとき、A→Cの反応熱は5+7＝12kJとなります。

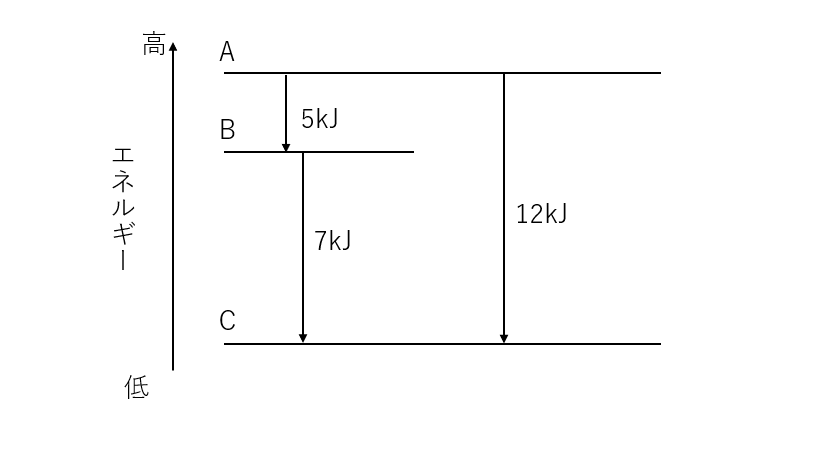
このように中間にどのような反応があったとしてもそれらの反応熱をすべて足してしまえば、最初から最後の化合物へ反応するときの反応熱を求められるということです。

では、ここでヘスの法則を使う問題を解いてみましょう。

問：二酸化炭素の生成熱を求めてみましょう。ただし、COの生成熱は111kJ、燃焼熱は283kJとする。

解説：まずは、COの生成熱と燃焼熱を表す熱化学方程式を書きましょう。

COの生成熱を表す熱化学方程式

$\mathrm{C(黒鉛)} ＋\frac{1}{2}\mathrm{O₂(気)}$

$＝ \mathrm{CO(気)} ＋ \mathrm{111kJ}$

COの燃焼熱を表す熱化学方程式

$\mathrm{CO(気)} ＋\frac{1}{2}\mathrm{O₂(気)}$

$＝ \mathrm{CO₂(気)} ＋ \mathrm{283kJ}$

この二つの式を足したときに、両辺にCO(気)があるのでそれを消したら以下のような式が得られます。

$\mathrm{C(黒鉛)} ＋\mathrm{O₂(気)}$

$＝ \mathrm{CO₂(気)} ＋\mathrm{394kJ}$

よって、二酸化炭素の生成熱が394kJだとわかりますね。ちなみに、この式からもわかるようにC(黒鉛)の燃焼熱と二酸化炭素の生成熱は同じ値になります。

このように、ヘスの法則を使って複数の式を一つの式にまとめることができます。問題としてみれば、ただ式を足して整理しているだけですね。