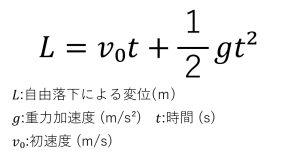ばねによる弾性力の働き
目次
フックの法則について
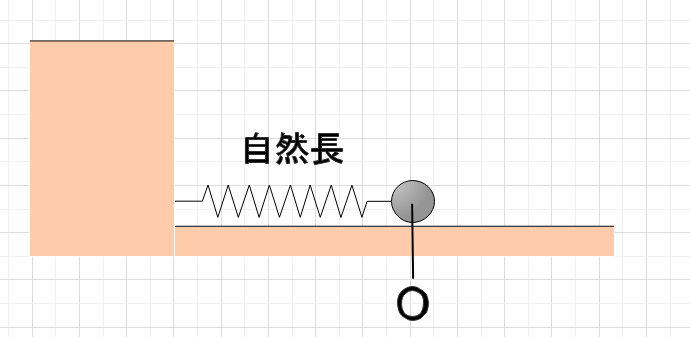
図1のようにばねが取り付けられているとき、ばねや物体に力が加えられなければ、ばねはある一定の長さに保っています。その時のばねの長さを自然長(もしくは自然の長さ)といいます。ばねを使った物理の問題では、伸びたり縮んだりしている状態のばねが自然長へと戻る力を使って計算します。そのような、変形した物体が元に戻ろうとする力のことを弾性力と言います。
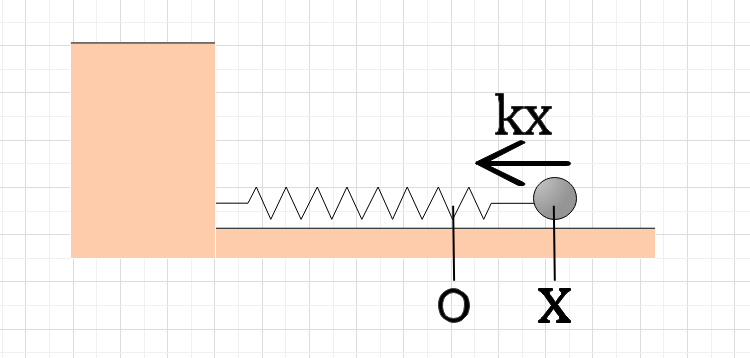
弾性力を求めるときには、自然長のときの物体の位置を原点として計算します。物体の位置が離れれば離れるほど弾性力は大きくなっていき、その力の方向は原点へと向かう向きになります。このような関係を表した式が以下の式1になります。
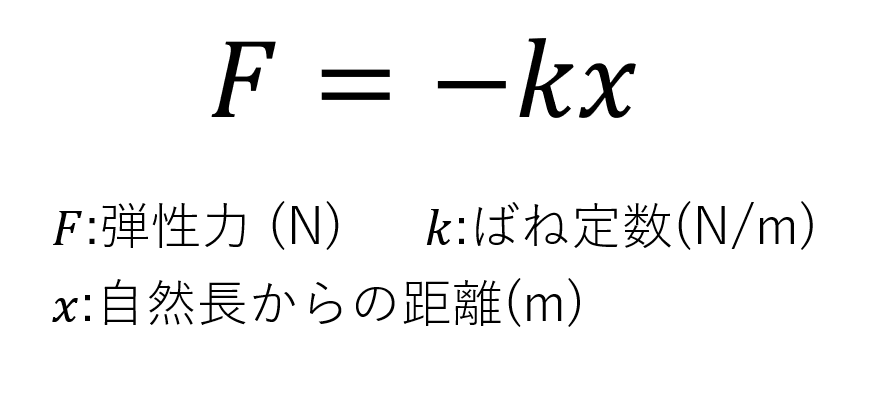
このような関係式をフックの法則といいます。ここでばね定数というものが出できますが、これはばねによって違う値を持っていて、簡単に伸びたり、伸ばそうとしてもなかなか伸びなかったりするようなばね自体の性質を表しています。右辺にマイナスがついていることに戸惑う人もいると思いますが、弾性力は元に戻る力なので、xの値がプラスならFは原点に戻る方向に働くためマイナスになります。反対に、xの値がマイナスならFは原点方向に働くためプラスにになります。つまり、xとFの符号は必ず逆になるため、右辺にマイナスがついているんです。
注)弾性力の大きさを求めよと問題で書かれている場合は、大きさなので絶対値で答えましょう。つまりマイナスは書くなということですね。
ばねが吊るされているとき
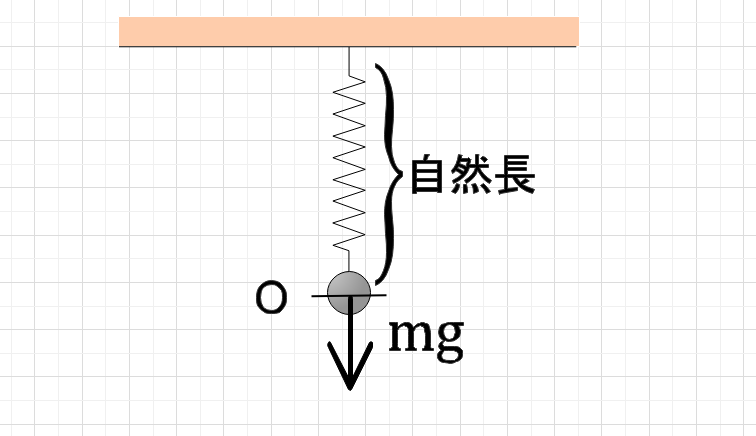
図3のようにばねが吊るされている場合は重力の分だけばねが伸びますが、その状態のばねの長さが自然長であることに注意してください。結局は、ばねを伸び縮みさせた後にどこの点に向かって戻っていくのかが重要なので、その点が重力で伸びたばねの端ならばその状態が自然長ということになります。
弾性力による位置エネルギー
自然長から伸びたり縮んだりしている状態のばねは位置エネルギーを持っています。そのような位置エネルギーを弾性力による位置エネルギーといいます。弾性力による位置エネルギーは以下のように求められます。(位置エネルギーについての詳しい解説についてはこちらから)
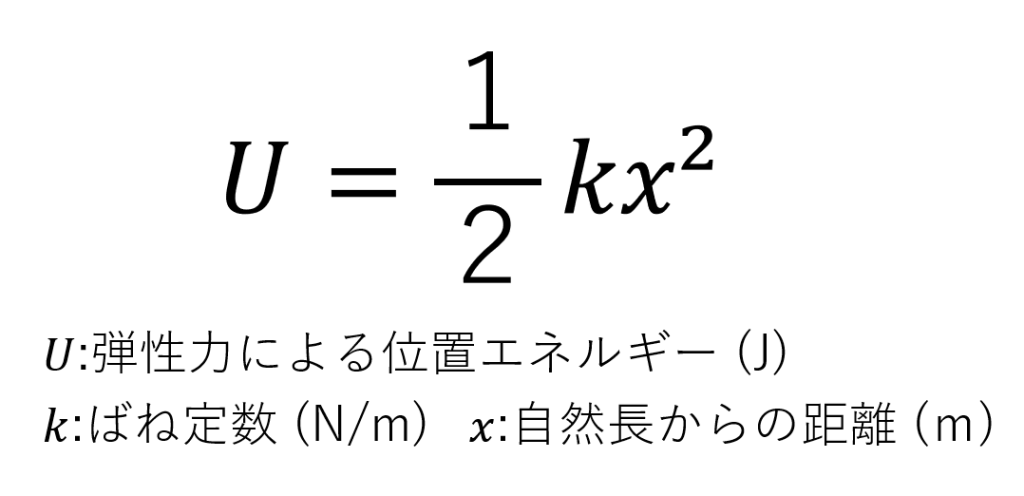
弾性力を使った問題
問題1 図2のようにばね定数kのばねの一端が固定されており、他端には質量mの物体が付けられていて、自然長よりxだけ伸びている。この状態の物体の加速度を求めよ。ただし、ばねの質量は無視し、摩擦はないものとする。
問題2 図2の状態から物体が初めて原点に移動したときの速度を求めよ。
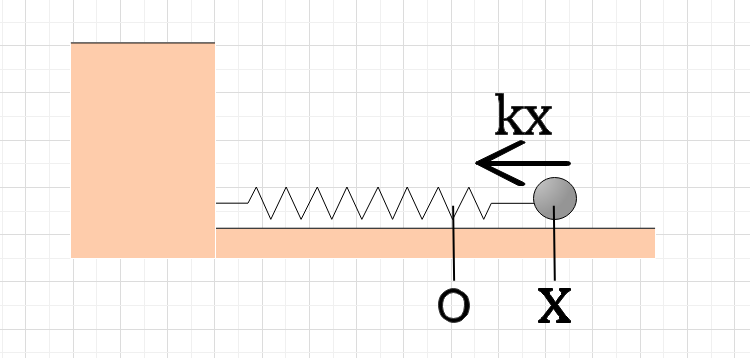
解説1 フックの法則より、物体に加わっている力はーkxとわかります。ここで、運動方程式のF=maのFにーkxを代入するとーkx=maになり、mを移項させるとa=ーkx/mになります。
よって答えは
となります。
解説2 原点からx離れているときの位置エネルギーは½kx²であり、原点に移動したときはその位置エネルギーが全て運動エネルギーに変化しているので、½kx²=½mv²が成り立ちます。両辺を2倍し、mを移項してルートをつけると、
となります。ここで終わってしまうと答えが2つ出てきてしまうので注意しましょう。図2の状態から初めて原点を通るときはマイナス方向に向かっていることが明確なのでこの場合の符号はマイナスであることが分かります。よって答えは、
となります。今回は速度を求める問題でしたが、問題文が速さを求める場合は、速さは速度の絶対値なため符号はプラスであることを覚えておいてください。