日常で割とよく使う・・・かもしれない「てこの原理」について解説!
物理の中でも特に原始的で扱いやすくてこの原理を今回は解説していきたいと思います。
目次
てこの原理、3つの点
まずは下の写真を見てください。
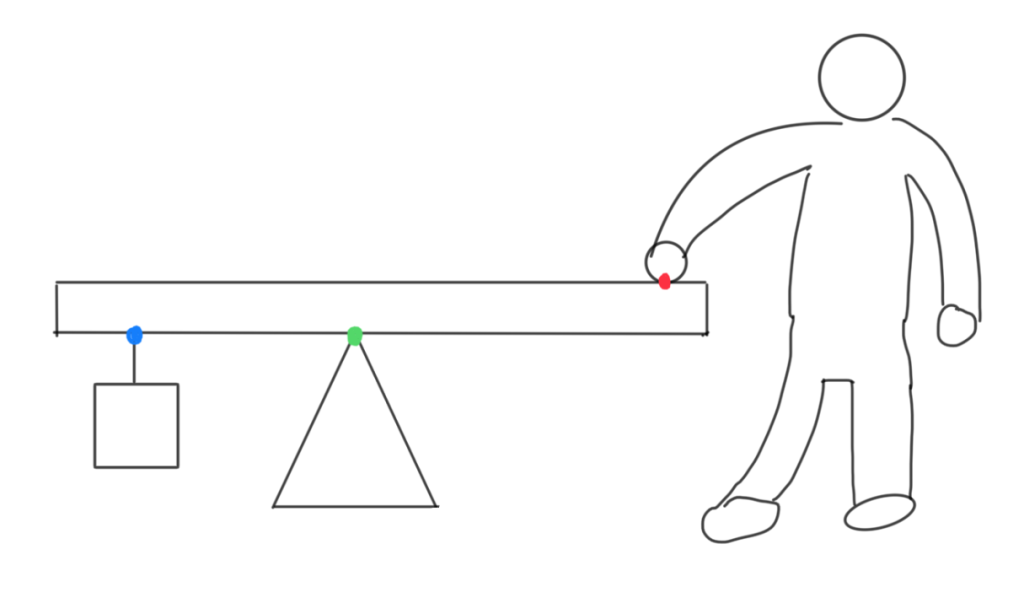
この写真は、右の人が、おもりが棒を引く力と同じ力を棒に加えて水平に保っているという状態です。
この時の緑の点を支点、赤の点を力点、青の点を作用点と言います。
距離の関係について
支点、力点、作用点について説明しましたがそれらの距離の関係についてお話ししたいと思います。
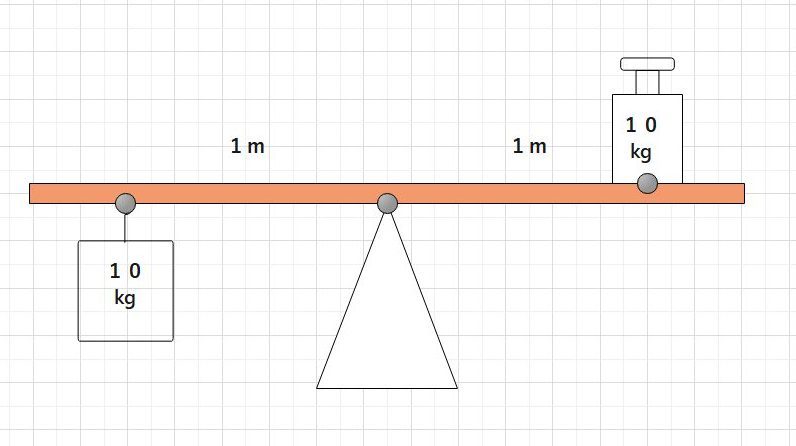
上の図では、それぞれの点の距離が1mと等しくなっています。この時、力点・作用点にかかる力も等しいので棒は水平に保たれています。また、次のような場合にも棒は水平に保つことができます。
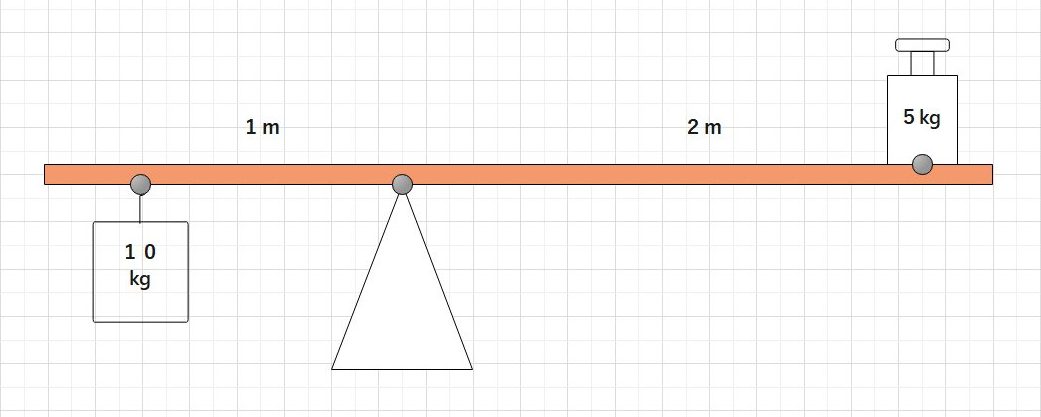
次の図では、力点と支店の距離が2mになった代わりに力点にかかる力が5kgになりましたが、
このような場合でも棒は水平に保たれます。
支点と力点の距離が比例すると水平に保つために必要な力は反比例します。
また、次のような場合もあります。
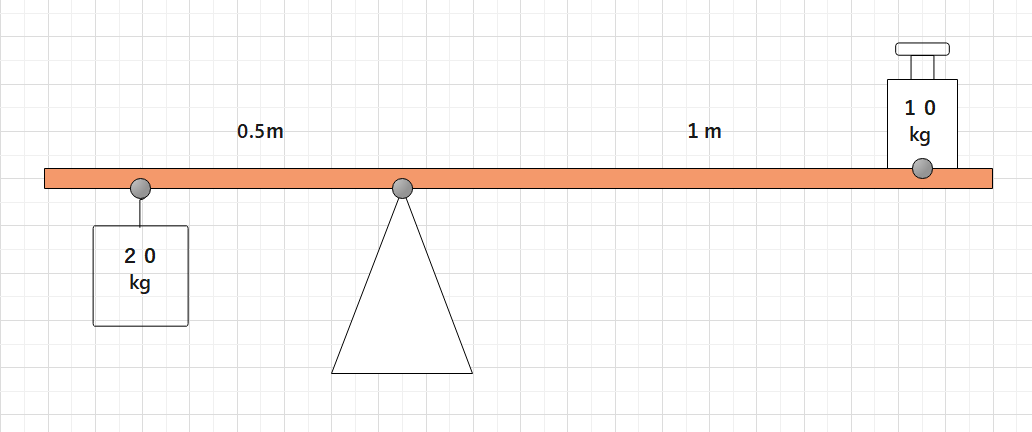
今度は、支点と作用点の距離が0.5mになり、作用点のおもりが20kgになりましたね。
このような場合でも棒は水平に保たれます。ここの関係も力点の時と同じで、
支点と作用点の距離が比例すると水平に保つためのおもりの重さは反比例します。
ここで、
支点と力点の距離をL₁
支点と作用点の距離をL₂
力点にかかる力をN₁
作用点にかかる力をN₂ として、これらの関係を式に表すと・・・
L₁×N₁=L₂×N₂
(水平時の場合)
つまり、重いものを持ち上げたいときは支点と作用点の距離を近づけるか、支点と力点の距離を離せばいいということですね。ここでは、作用点・支点・力点の順で説明していますが、これらの点の順を変えてもてこの原理の関係性は成り立ちます。
身近に使われるてこの原理
はさみ

日常的に使うてこの原理といえばこれですかね。
紙を切るときは支点の近くで切りますよね、
はさみの先端で切ったときと支点の近くで切った時の切れ味が違うのがわかると思います。
自転車(自動車)のハンドル

これにもてこの原理が使われています。
ハンドルを持つ位置と支点の位置も離れているし、支点とタイヤの位置はかなり近いです。
ホチキス
これは支点が真ん中になく、力点が真ん中に来ているパターンです。
栓抜き
これは作用点が真ん中に来ています。
どうだったでしょうか、意外と単純で日常でもたくさん使われているのがわかっていただけたでしょうか。緊急時などのときに大きな力が必要な場合に、てこの原理を使う機会があるかもしれません。地震でドアが開かなかったときはちょっと開けた隙間に鉄の棒を突っ込んで開けたりなど、覚えておけば便利かもしれませんね。