力を加えるという事

　　身近な力と言えば、重力や摩擦力はよく聞きますよね、これらの力が物体に働いたときどのような挙動をするのかを解説していきたいと思います。

目次

• 力は物体に加速度を与えている
• 摩擦力について
• 物理における仕事
• 仕事率とは

力は物体に加速度を与える

　止まっている状態のビー玉にデコピンしたらもちろんビー玉は飛んでいきます。最初は止まっていたはずのビー玉が動いたわけだから、加速度が働いているのがわかりますよね。このような現象をちょー簡単な式で表すことができるんです。

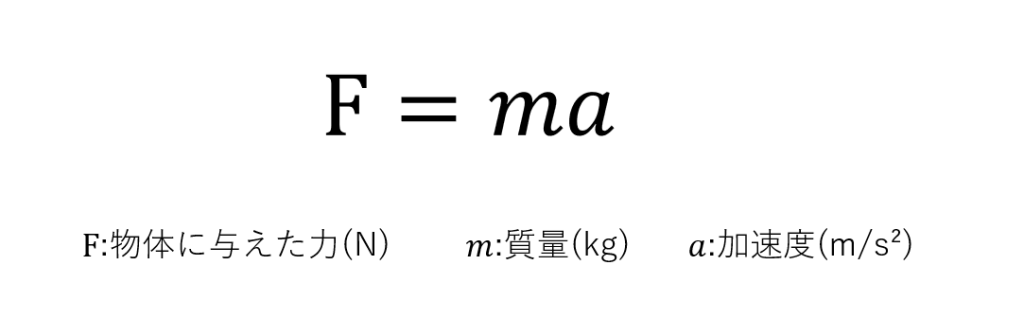
　加えた力と加速度は比例し、質量と加速度は反比例することがわかります。加えた力はニュートン(N)という単位で表されます。この式だけを見ると、どんな重い物体にも力を加えると少しは動くはずですが、車は少し押しただけじゃピクリとも動きません。ではなぜ動かないんでしょうか？それには皆さんおなじみの摩擦力が関係しています。ということで、次は摩擦力について解説していきたいと思います。

摩擦力について

　摩擦力もデコピンと同じように物体に力を与えるので物質に加速度を与えます。とはいえ皆さんもお分かりの通り、摩擦力によって発生する加速度は速度が増加するプラスの加速度ではなく、速度が減少するマイナスの加速度なので、どれだけスピードを出している車でもアクセルを踏むのをやめれば、ブレーキをかけなくてもいつかは止まります(ブレーキはちゃんとかけてください)。

　図２で急に出てきた動摩擦係数と静止摩擦係数ですが、摩擦力ってものによって違いますよね、表面がざらざらしているものだったら摩擦力が大きいし、表面がつるつるしてたり形が丸かったら摩擦力が小さいです。このような、形状や材質によって特定の値を持つ係数です。

　というわけで、摩擦力がどのように求められるのか見てみましょう。

注）以下の式は平面上にある物体でのみ使える式です。

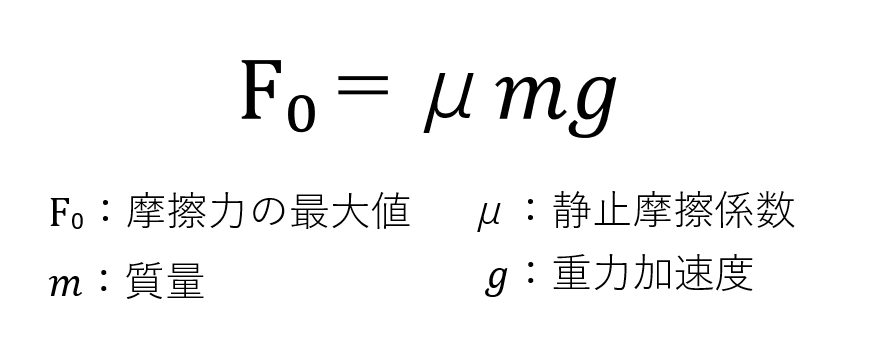
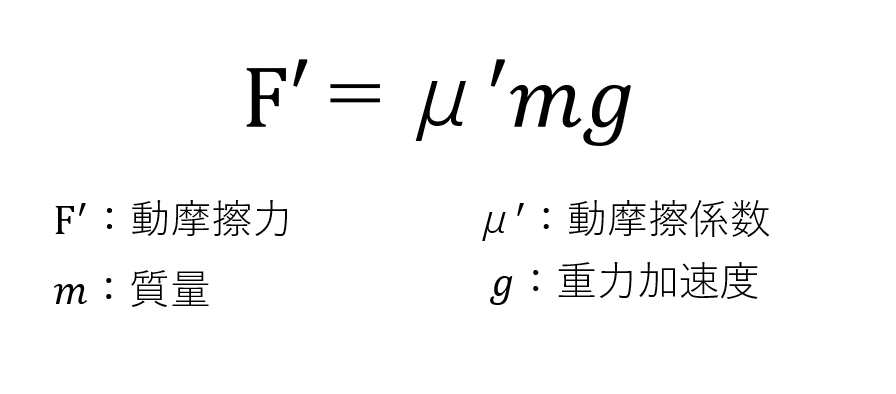
　ここで注意してほしいのは、静止しているときに発生している摩擦力はいつもF₀ではなく、物体が動かないように、加えられた分と同じ摩擦力が発生します。そしてF₀よりも強い力を加えたとき物体は動き出し、物体の摩擦力は動摩擦力に変化します。

物理における仕事

　物理における仕事をいくら行ったとしてもお金は手に入らず、むしろ体の中のエネルギーが無くなってしまいます。では、何をしたらどのくらいのエネルギーを消費するのか、それを式で表したものが以下のものになります。

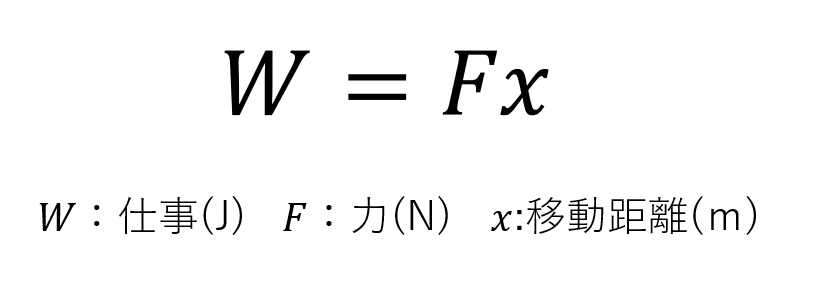
　仕事はJ(ジュール)という単位を使って表します。4.2Jで1gの水が1°C上昇するということを覚えておくとイメージしやすいかもしれません。仕事が発生する条件として、力の向きに物体が移動しなければいけなく、斜めに力が働いている場合は移動方向に力を分解して計算しなければいけません。例えば、以下のような場合があったとします。

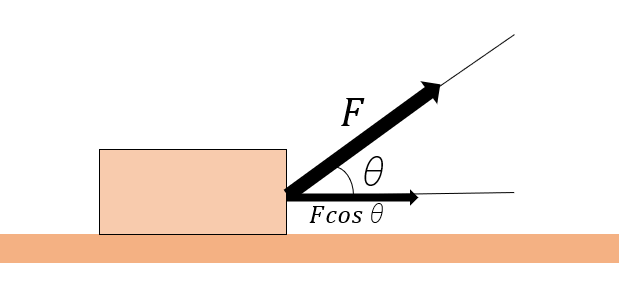
　このように物体に斜めにFの力が働いていますが、実際の物体の移動方向は地面に平行の右向きです。そのため、物体に働く力を移動方向に分解しなければいけません。力と移動方向のなす角はθですので、三角関数を使うことで移動方向に働く力はFcosθであることがわかります。

力の大きさが変化したときの仕事の求め方

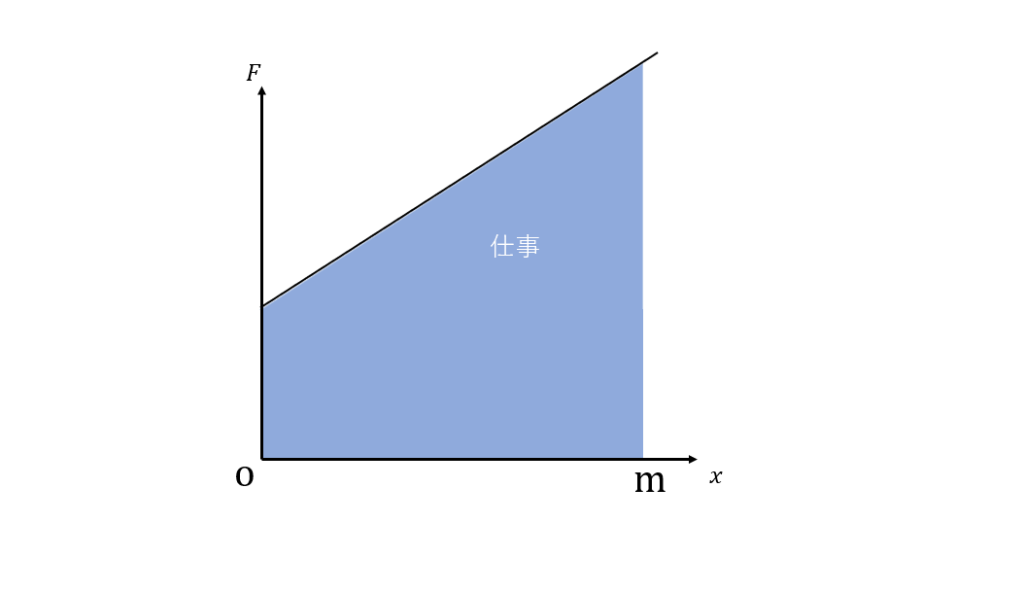
　力の大きさが変化しているときは図５のように単純に求めることはできません。どのように求めるのかというと、グラフ中の面積を求める方法です。これは加速度があるときの距離の求め方でも使っていましたね。(その時の記事はこちらから)

仕事率とは

　少し元々の本題と離れてしまいますが、せっかく仕事の話をしたのでついでに仕事率の話をしようかと思います。仕事率というのは、複数の仕事を比較するために使われるもので、下の式のように仕事を時間で割って単位時間当たりの仕事にしたものです。

　仕事率はW(ワット)という単位を使って表します。似たような単位に、日常的に使う電力量を表すkWh(キロワット時)があります。この単位は1kWの仕事率で１時間に供給する仕事を表していて、仕事率に時間をかけているため、これは仕事率ではなく仕事の単位であることに注意してください。