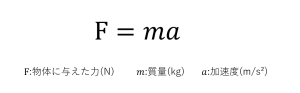速度と加速度
目次
速さと速度の違い
速さと速度って一見同じ意味に見えて実は違うんですよね。簡単に言うと、速さには向きがなくて速度には向きがあるということです。言葉だけで聞いてもいまいちよくわからないですよね・・・。ということで図を見ながら理解していきましょう。
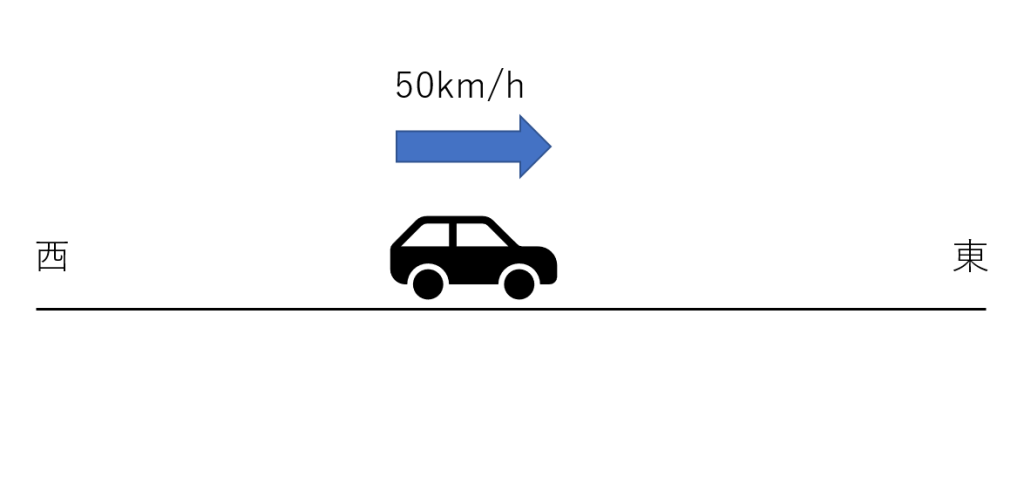
図1のような、東の方向に50km/hで進んでいる車があったとしましょう。この場合の車の「速さ」は単に50km/hになりますが、これを「速度」で表すとなると、東向きに50km/h(または西向きに-50km/h)となります。速度は物体がどの方向に進むか指定しているんです。速さは速度の絶対値と覚えておけば大丈夫です。
速度と距離の関係
速度は単位時間あたりに進んだ距離を表しているので、「移動した距離/移動した時間」で求めることができます。もちろんその間に速度が一定かどうかはわからないので、その時間内の平均の速度となります。そのため、速度の単位は「距離の単位/時間の単位」で表されます。時速などを使って表すときもありますが、時速などは「/時間の単位」の部分を担っていると覚えてください。そういうわけで、速度の単位が分かったということで距離との関係も見えてきましたね。

速度に時間をかけると距離になります。すごい当たり前のことですが、これが加速度の話になると少し変わってくるんです。
加速度と距離の関係
まず、加速度について説明していきましょう。加速度というのは単位時間あたりに変化した速度の量を表しています。そのため、加速度はm/s²や、km/h²などのように速度をさらに時間で割った単位になります。ここで注意しなければいけないのは、見かけ上の加速度の単位がこのようになっているからと言って、加速度を求めるときに単純に時間で割ってはいけません。距離の単位を時間の単位で2回割るというより、速さを時間で割っていることを意識してください。
加速度は基本的にaを使って表されます。加速度が距離を時間で二回割った単位だからと言って、距離を加速度で求めるときにat²になることはありません。実は次のようになります。
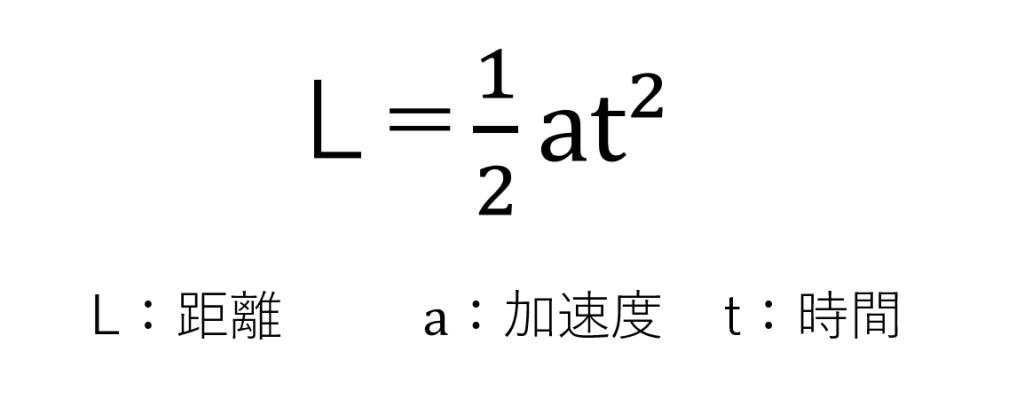
このようになってしまう理由は次の面積を使って距離を求める方法で解説していきます。
面積を使って距離を求める
等速直線運動の場合
まずは簡単に、等速直線運動の場合について考えていきたいと思います。その時の速さと時間の関係を表すグラフは図2のようになります。このグラフを時間=tで囲ってみた時、青色の四角形ができると思います。
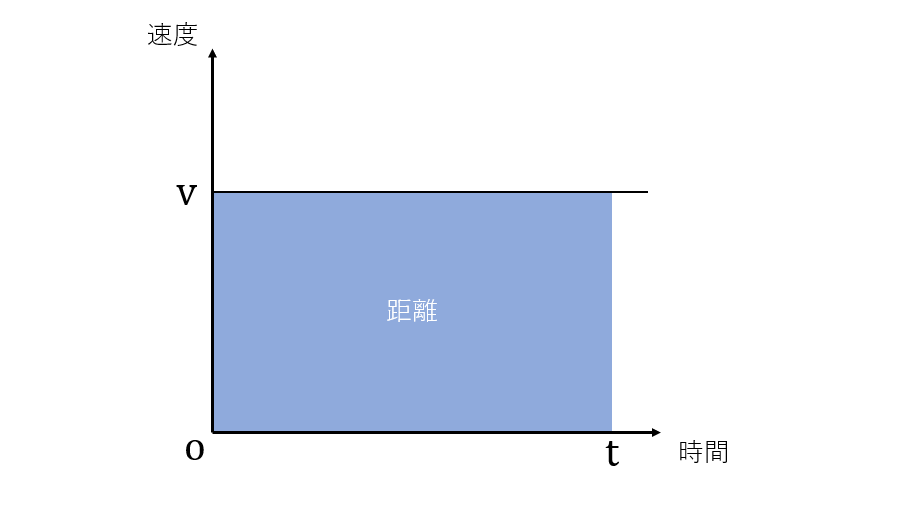
では、この四角形の面積はどのくらいかというと、縦の長さはv、横の長さはtということで、vtと表すことができます。これは式1の距離と一致します。このように、グラフの軸と関数の線、時間=tの線で囲まれた面積は距離を表しているということが分かります。この方法を使って、等加速度運動の場合について考えていきましょう。
等加速度運動の場合
加速度がaで初速が0の時の、等加速度運動をしている時の時間と速度の関係を表すグラフは図3のようになります。時間とともに速度が増加しているので、斜めになった線となっています。このグラフもさっきと同じように、時間=tで囲むと今度は青色の三角形ができます。
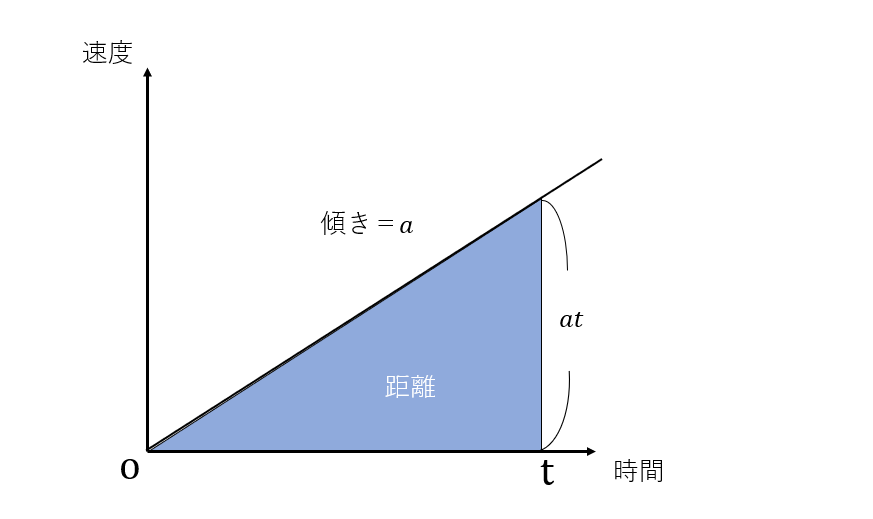
この面積を求めると、縦の長さはat、横の長さはtですが、三角形なので½を掛けると面積は½at²で、式2の距離と一致します。このようにして等加速度運動の距離の求め方は式2のようになるんですね。
余談ですが、速度を求めるときに使うtと、加速度を求めるときに使うtは別物であると理解してたらこんなことしなくてもよかったの知れませんが、こういう考え方もあるということを覚えておいてみてください。(結構有名な考え方ですしね。)