力の合成と分解
力の合成と分解は、物体の挙動を分かりやすくするために非常に重要なことなので覚えておきましょう。
目次
力の足し算と引き算
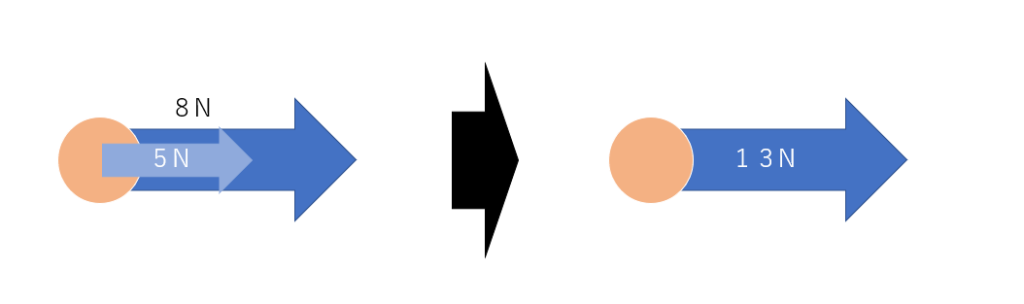
図1のように、球体に8Nの力と5Nの力が同じ方向に加えられている状況があった場合、結局はその方向に13N加えられていることと同じことが分かります。
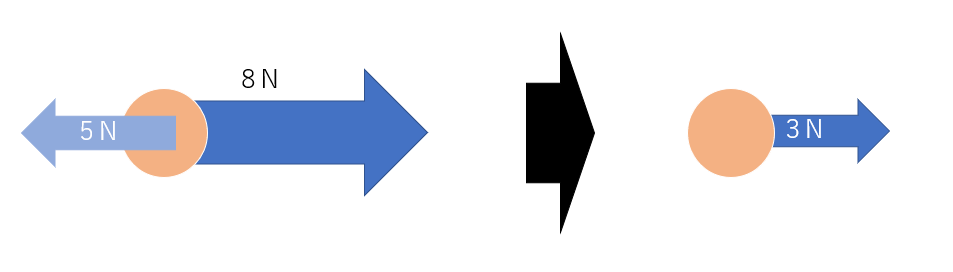
次に、図2のような二つの力(5Nと8N)が互いに真逆の方向へ働いていた時、今度は力が打ち消しあうため引き算し、右方向に3Nの力が働きます。
ただ、力の方向の基準を右方向にすることで、左方向に働く5Nを右方向にとってのー5Nとみなし、足し算する形でも求めることができるので、自分の感覚に合った方法を選んでみてください。
このように、複数働く力が平行であった時の力の合成は、単純な足し算引き算で表すことができますが、複数働く力が平行ではない場合が出てきたときはそう簡単にはいきません、次はそのような場合について説明していきたいと思います。
力の矢印を合成する
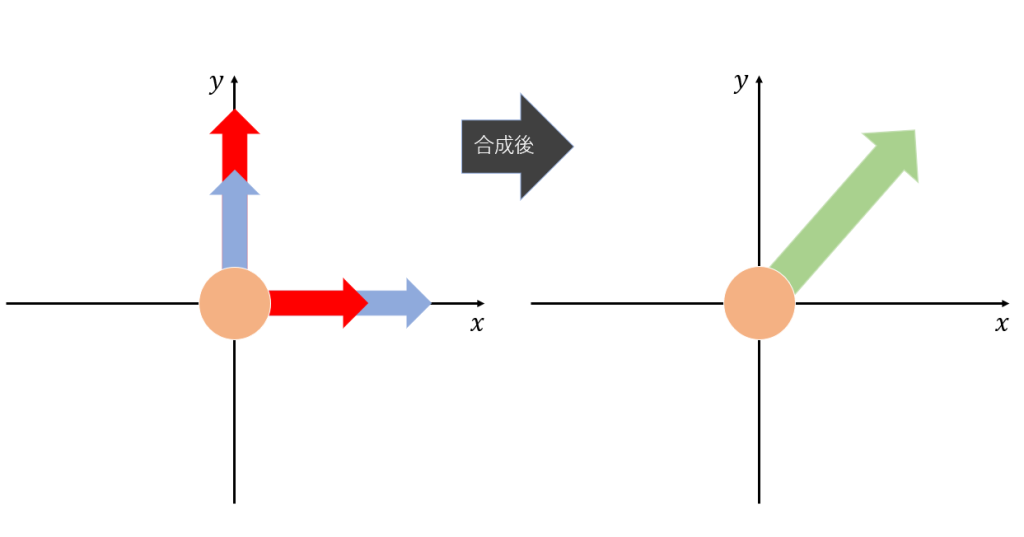
複数の力が平行ではない時、単純な足し算引き算では求めることはできないし、力の方向の求め方も少し変わってきます。図3のような、力の矢印が互いに垂直になっているような状況があったとします。
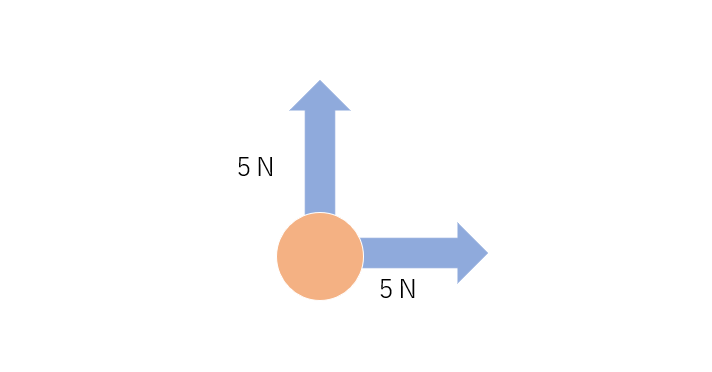
力を合成する手順は実は簡単で、矢印の始点と終点をつなぎ合わせて1つの線にして、その線の始点と終点の直線が合成された矢印になります。わかりやすく図に示すと図4のようになります。
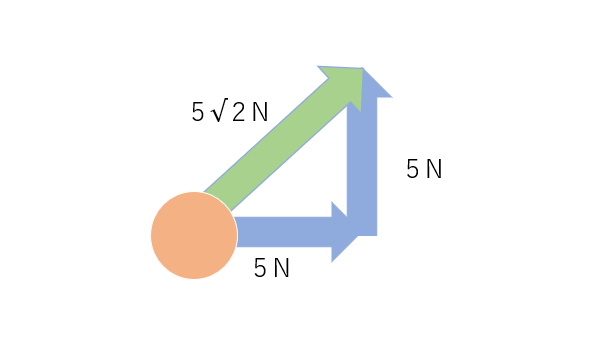
このように青色の矢印をつなげることによって、合成された緑色の矢印を作ることができます。緑色の矢印の力の大きさを求めるときは、力の大きさ=直線の長さとみなし、三平方の定理で求めることができます。
この方法を使うことによって合成された力の方向はわかりますが、ある2つの力が垂直に交わっていない時(図5のような場合)は三平方の定理を使うことができないので、この次に話す力の分解が重要になります。
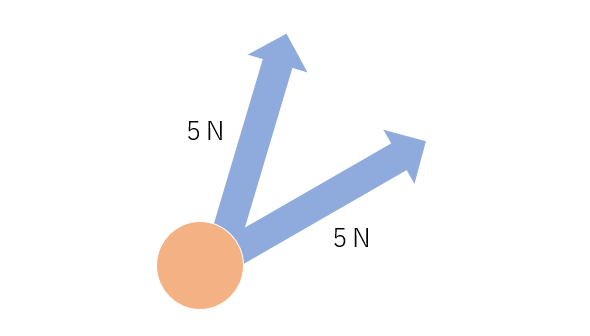
力の矢印を分解
斜めに働く力が横方向と縦方向にどのような影響を与えるのかを分かりやすくするために、力の矢印を水平方向と鉛直方向(グラフ上ならx方向とy方向)に分解することがあります。図6のようなxyグラフ上にある力の矢印を分解してみましょう。
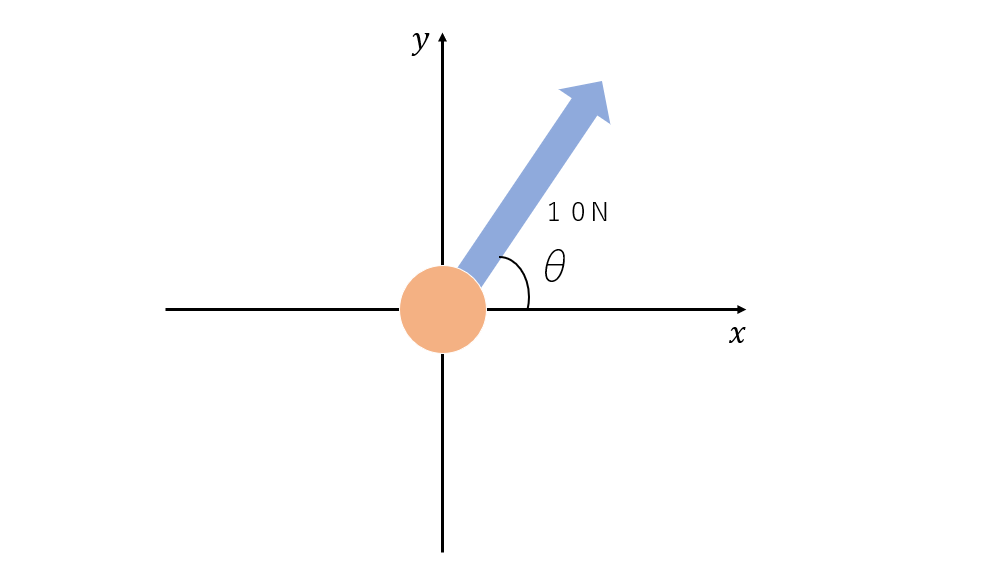
力の分解をするときは三角関数を使います。上のでも話しましたが、「力の大きさ=矢印の長さ」と考え、矢印の方向とx軸とのなす角のθを使い、xy軸それぞれの方向に分解すると図7の赤色の矢印のようになります。
三角関数の使い方についてはこちらの記事を参考にしてみてください。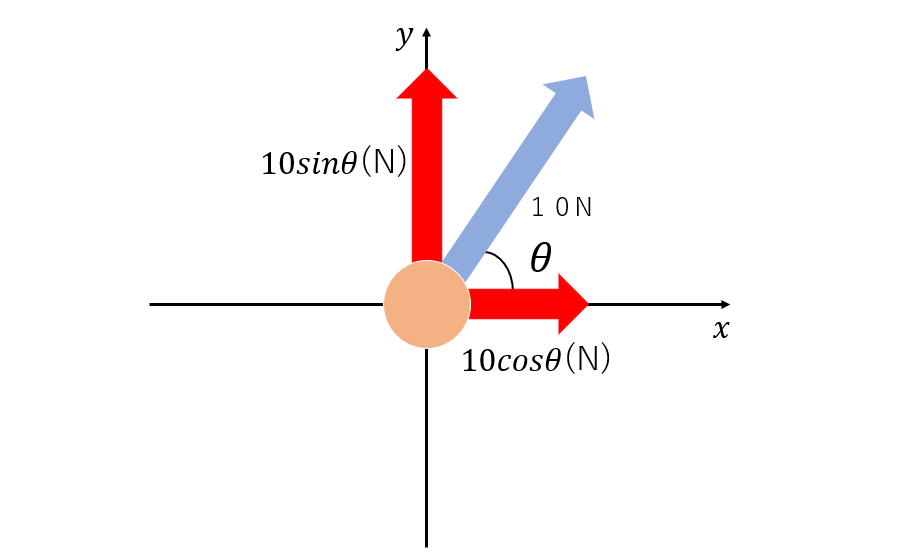
このように三角関数を使って力の矢印を分解することができます。例えば、ななめに投げたボールが何秒後に落ちるのか、落ちた地点は何m先なのかが分かりやすくなったりなど使える場面はたくさんあります。
力の分解を学んだところで、図5の力の大きさを求めてみます。ここまできたらどうやるのか察している人も多いと思います・・・、そうですね、二つの力を分解し、同じ方向の矢印を足して三平方の定理で大きさを求めます。