運動量と力積
解説1
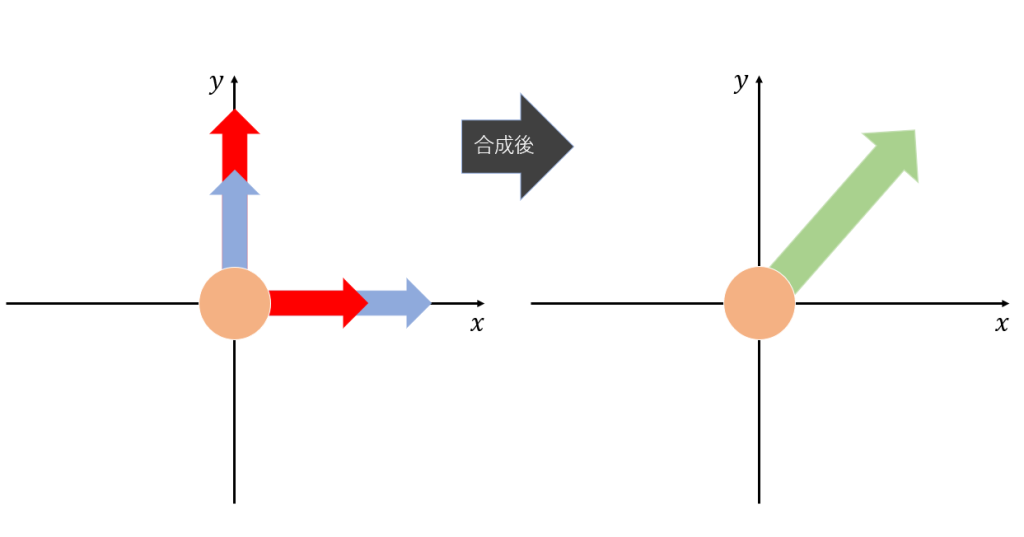
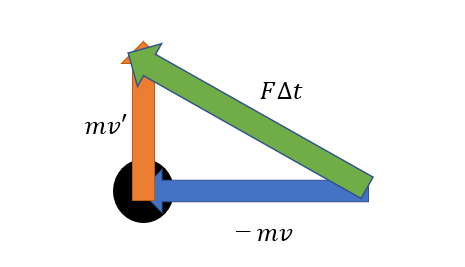
式2を使って考えてみると、ベクトルはマイナスを掛けたら方向が逆転するので を表すベクトルは図3の青色の矢印のようになります。そして、二次元でのベクトルの合成はベクトルの始点と終点をつなぎ合わせ、つながった線の始点と終点で直線を引くことで各ベクトルを合成したベクトルが完成するので、そうやって合成したものが緑色のベクトルで、それが を表します。
また、 の大きさはベクトルの長さに反映されるので、他二つのベクトルの長さを使い、三平方の定理を用いてその値を求めることができます。ということで を代入し、三平方の定理を用いると のベクトルの長さは とわかりましたね。これが の値になります。
式2を使って考えてみると、ベクトルはマイナスを掛けたら方向が逆転するので を表すベクトルは図3の青色の矢印のようになります。そして、二次元でのベクトルの合成はベクトルの始点と終点をつなぎ合わせ、つながった線の始点と終点で直線を引くことで各ベクトルを合成したベクトルが完成するので、そうやって合成したものが緑色のベクトルで、それが を表します。
また、 の大きさはベクトルの長さに反映されるので、他二つのベクトルの長さを使い、三平方の定理を用いてその値を求めることができます。ということで を代入し、三平方の定理を用いると のベクトルの長さは とわかりましたね。これが の値になります。
ベクトルの合成は力の合成と似ているので、力の合成についての記事を紹介します。よかったら見ていってください。
基本的には式4の運動量保存則を使えば問題ないです。式4に代入していくと
となり、この式を整理し の値を求めると
と求めることができます。
こんな感じで直線上の運動量の計算はできますが、これが二次元の話になった時、 軸方向と 軸方向の二つの運動量保存則の式をたてて計算しなければならないことを覚えておいてください。