運動量と力積
目次
運動量について
同じ質量を持っている物体なら速度が速いほうが、同じ速度を持っている物体なら質量が大きいほうがその物体のもつ力が大きく感じますよね。運動量はそういった物体の運動の勢いを表すための量になります。では、さっそく運動量がどうやって求められていくのか見ていきましょう。

運動量は質量×速度で求められ、単位はkg・m/s(キログラムメートル毎秒)で表されます。
力積について
力積は運動量の差を表す値です。物体の運動方向に力を加えればその物体の運動は激しさを増し、力を加える時間を増やせば増やすほどさらに運動は激しくなりますよね。力積は、そういった物体にどれだけ運動量に影響を与えたのかを示し、で表されます。
運動量と力積の関係は以下のように表されます。

こんな感じでわかりやすく力積は運動量の差で表されますが、ここで注意してほしいのは、式の中にあるそれぞれのベクトルは必ずしも同じ方向とは限りません。また、同じ作用線上にあるわけでもなく、角度がついているときもあるので単純な数値の引き算では力積を求めれないこともあり、そういう場合は図を用い、ベクトルの引き算を使って求めていくこともあります。言葉で説明しても難しい部分はあると思うので、一通り説明した後問題を通して解説していきたいと思うのでよければ最後まで見ていってください。
運動量保存則
二つの物体A,Bが互いに衝突したとき、もちろんそれぞれの物質は力積を受けます。物質Aが受けた力積をとしたとき、作用反作用の法則により、物質Bの受ける力積はとなります。衝突前後の物体A,Bの運動量の変化と、それぞれの受けた力積との関係を式に表すと以下の二つの式が出来上がります。
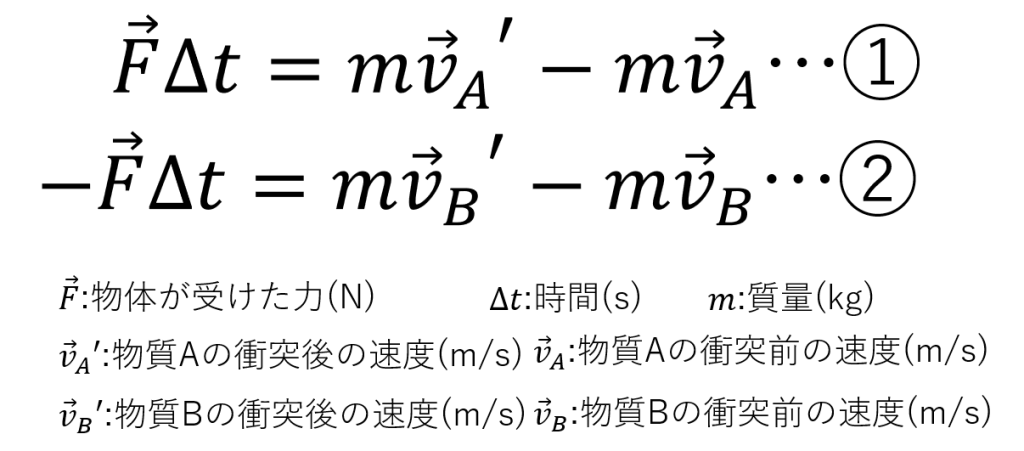
そしてこの式①,②を足して整理すると以下のような式になります。
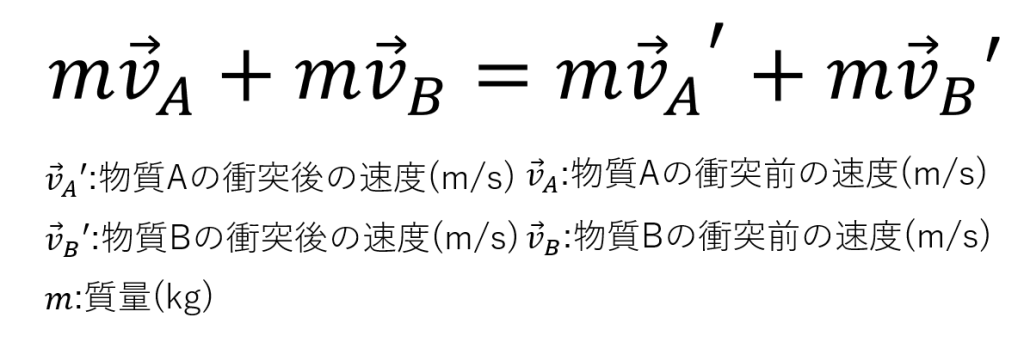
ということで、この式からわかる通り衝突前後で物体A,Bの運動量の和は変化しないことが分かります。これが運動量保存則を表す式になるんですが、この式が成り立つためには少し条件があります。それは、衝突した物体同士が内力を及ぼし合うだけで外力を受けていない、もしくはその外力がつりあっていることです。内力というのは物体同士が互いに及ぼい合う力で、衝突直後の物体A が物体Bに与える力、物体Bが物体Aに与える力を示します。それに対し外力は物体A,B以外から受ける力(重力や摩擦力など)を示します。外力によって速度が変化してしまうため運動量も変化してしまい、結果的に運動量保存則が成り立たなくなってしまいます。
練習問題
ある一定の運動量 をもった物体が力積を受けたことにより、図1のように運動量が変化した。このとき、受けた力積の方向を矢印を用いて示せ。また のとき、受けた力積 の値を求めよ。
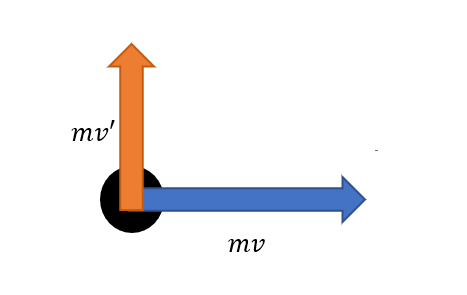
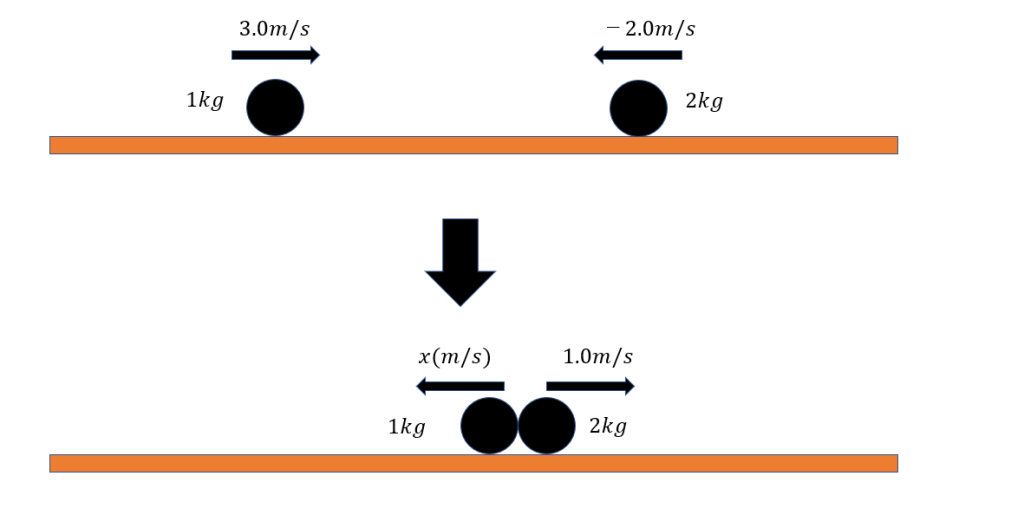
図2のように、質量1kg、速度が3.0m/sで進む物体Aと、質量2kg、速度が-2.0m/sで進む物体Bがある。これらの物体が衝突した時、物体Bの速度は1.0m/sに変化した。そのときの物体Aの速度 を求めよ。
解説は次のページへ